[물리전자] 2-3. 자유공간과 무한전위우물(Infinite Quantum Well) 내에서의 전자운동
지난 포스팅에서 간단하게 언급하였듯이, 이번 포스팅에서는 자유 공간에서의 전자 운동, 그리고 무한전위우물(Infinite Potential Well)에서의 전자운동을 이론적으로 증명해보고자 합니다. 그러기 위해선 각 상황에서 Schrodinger Equation을 풀어내야 합니다. 이를 위해 간단하게 Schrodinger Equation이 어떤 형태였는지 다시 한번 보고 넘어갑시다.
$$ {d^2 \over dx^2}\psi(x) - {2m \over \hbar^2}(E - V)\psi(x) = 0$$
이제 이 식을 활용하여 여러가지 상황에서의 전자 거동을 알아봅시다.
자유 공간의 전자
먼저 자유 공간에 존재하는 전자에 대해 알아보겠습니다. 진공 중에 있는 전자는 고체에 들어있는 원자핵하고는 전혀 무관합니다. 즉 외부로부터 어떠한 힘도 받지 않는 전자를 의미합니다. 이런 전자의 움직임을 생각해봅시다.
외부로부터 어떤 힘도 받지 않기 때문에 자유 공간의 전자가 갖는 Potential은 0입니다. 사실 자유공간이면 x, y, z 방향 모두 고려해 주어야 하는데 우리는 x축 방향 고려하겠습니다. 따라서 다음과 같은 식이 성립합니다.
$$ V(x) = 0 $$
이 조건을 Schrodinger Equation에 대입합시다.
$$ {d^2 \over dx^2}\psi(x) + {2mE \over \hbar}\psi(x) = 0 $$
이 식을 풀기 위해 ${d \over dx} = D$라고 합시다.
$$ \left({D^2 + {2mE \over \hbar^2}}\right) \psi(x) = 0 $$
이것을 풀면 다음과 같은 해를 얻을 수 있습니다.
$$ D = \pm i\sqrt{2mE \over \hbar^2} $$
따라서 Wave Function $\psi(x)$는 다음과 같습니다.
$$ \psi(x) = Ae^{i\sqrt{2mE \over \hbar^2}x} + B e^{-i \sqrt{2mE \over \hbar^2}x} $$
여기서 루트안의 ${2mE \over \hbar^2}$을 k라고 정의합시다.
$$ k = \sqrt{2mE \over \hbar^2} $$
여기서 k를 Wave Number라고 합니다. 위의 식에서도 알 수 있듯이 k는 운동량에 관한 식으로도 표현할 수가 있습니다. 에너지 E가 운동에너지라는 것을 이용해 유도하면 다음과 같습니다.
$$ k = \sqrt{2m\left({{1\over2}mv^2}\right) \over \hbar^2} = \sqrt{m^2v^2 \over \hbar^2} = {mv \over \hbar} = {p \over \hbar}$$
이것을 통해 운동량 p를 Wave number k와 $\hbar$로 구할 수가 있게 되었습니다.
$$ p = \hbar k $$
그런데 여기서 $\hbar$는 플랑크 상수를 $2\pi$로 나누어준 값이기 때문에 p와 k는 서로 비례관계입니다. 또한 이를통해 k는 운동량하고 같은 단위를 갖는다는 것을 알 수 있습니다.
다시 돌아와서 자유 공간에서 Wave Function을 구한 것을 정리해보면 다음과 같습니다.
$$ \psi(x) = Ae^{ikx} + Be^{-ikx} $$
위에서 구한 것을 이용하여 $\Psi(x,t)$를 표현할 수 있습니다. $\phi(t)$는 $e^{-iwt}$로 이므로 다음과 같이 표현됩니다.
$$ \Psi(x,t) = \psi(x) \phi(t) = Ae^{i(kx - wt)} + Be^{-i(kx + wt)} $$
이 식이 갖는 의미를 생각해봅시다. $Ae^{i(kx - wt)}$의 경우는 x방향으로 진행하는 파, $Be^{-i(kx+wt)}$는 -x 방향으로 진행하는 파를 의미합니다. 이것은 전자가 있으면 왼쪽으로 갈수도, 오른쪽으로 갈 수도 있다는 것을 의미하죠.
그렇다면 진행 속도는 어떻게 될까요? 위 식에서 입자의 진행속도는 $kx - wt =0$이 되는 지점일 것입니다. 이거의 값이 어떻게 되냐면 속도라는 것은 거리를 시간으로 나누어 준 것이 되기 때문에 다음과 같은 수식을 세울 수가 있습니다.
$$ {x \over t} = {w \over k } = C$$
이 식을 k에 대해 정리해봅시다.
$$ k = {w \over c} = {2\pi\nu \over c} = {2\pi \over \lambda} = {2\pi \over h} p = {p \over \hbar} $$
아까 위에서 구했던 $p = \hbar k$와 같은 식이 만들어졌습니다. 이것은 어떤 파동이 있는데 그것의 속도를 구해보니 k라는 것의 값이 $\hbar p$가 나온다는 것이죠.
이제 입자가 자유공간에서 +x 방향으로 진행하는 상황에 대해 식을 구해봅시다. +x 방향으로만 진행한다는 것은 B = 0이 된다는 것을 의미합니다.
$$ \psi(x) = Ae^{ikx} $$
만약 이런 입자의 에너지가 특정 값으로 고정이 되어있다면, 이 에너지는 운동량으로써 나타나게 됩니다.
$$ E = {1\over2}mv^2 = {p^2 \over 2m} $$
즉 입자의 에너지가 고정되면, 운동량 또한 특정 값으로 고정이 됩니다. 운동량의 오차가 없다는 것이기 때문에 다음과 같은 식이 성립합니다.
$$ \Delta p_x = 0 $$
그러면 운동량이 일정하기 때문에 k 또한 일정한 값으로 고정이 됩니다. 즉 k가 상수가 되는 것이죠. 그렇게 되면 다음과 같이 Wave Function을 표현할 수 있습니다.
$$ |\psi(x)|^2 = Ae^{ikx}(Ae^{ikx})^* = A^2$$
즉 더이상 Wave Function이 x의 함수가 아니게 됩니다. 따라서 어떤 전자가 발견될 확률은 모든 거리에서 일정하게 됩니다. 그래서 $\Delta x$는 무한대로 가게 됩니다. 다시 전체적인 그림을 보게 되면 $\Delta p_x$가 0이 되니 $\Delta x$가 무한대가 되었습니다. 이것이 바로 Heigenberg의 Uncertainty Principle입니다.
이것을 수학적으로 이야기하면 +x 방향으로 움직이는 전자파는 어디에 존재할지 알 수가 없다는 것이죠. 전자가 어디 존재하는지 명확하게 짚을 수가 없다는 것입니다. 자유공간에서 전자는 그냥 해본 것이고 반도체에서는 큰 의미가 없습니다. 반도체에서 의미 있는 것은 원자 핵 속에 들어있는 전자의 거동입니다. 원자핵이 배열되어 있으면 원자핵의 (+) Charge 때문에 Potential이 형성이 됩니다.
그래서 이제 할 것은 이런 Potential 장벽이 있을 때 전자는 어떻게 거동하는지 살펴보아야 합니다.
Infinite Quantum Well
반도체 내에서 전자의 거동은 원자핵의 영향을 크게 받습니다. 따라서 Potential이 항상 0인 자유 공간이 아니라 Quantum Well이라는 Potential Barrier에 막혀있는 공간에서의 거동을 구해야 합니다.
Quantum Well에서 전자의 거동을 해석할 때, 가장 기초적인 예제로 소개되는 것이 Infinite Quantum Well Problem입니다.

양 끝에 Potential이 $\infty$인 공간이 존재하기 때문에 Infinite Quantum Well이라고 부릅니다. 하지만 모든 구간에서 Potential이 $\infty$가 아니고, $x =0$ 부터 $x = L$까지는 Potential이 0인 공간이 존재합니다. 이 때, Potential Barier 내부에 존재하는 질량이 m인 입자의 거동을 Schoringer Equation을 통해 해석하는 문제가 되겠습니다.
먼저 Potential이 $\infty$일 때를 생각해봅시다.
Schrodinger Equation : $ {d^2 \over dx^2}\psi(x) - {2m \over \hbar^2}(E - V)\psi(x) = 0$
Potential이 $\infty$이면 $\psi(x)$가 0이 아닌 유한한 값을 갖는 경우 Schrodinger Equation은 절대로 성립할 수 없기 때문에 Schrodinger Equation을 만족하는 $\psi(x)$는 0밖에 없습니다. 이것은 Infinite Quantum Well에서 Potential이 $\infty$인 구간에서는 전자가 존재할 수 없다는 것을 의미합니다.
그러면 이제 구해야 할 것은 Potential이 0인 구간에 전자가 어떻게 존재하는가 입니다. 이것에 대해 Schrodinger Equation을 풀어봅시다. 이 구간에서는 $V = 0$이므로 이를 대입하면 다음과 같습니다.
Schrodinger Equation : $ {d^2 \over dx^2}\psi(x) - {2m \over \hbar^2}E\psi(x) = 0$
이렇게 되면 자유 공간에서 움직이는 전자와 같은 식이 됩니다. 따라서 일반해는 다음과 같습니다.
$$ \psi(x) = Ae^{i\sqrt{{2mE \over \hbar^2}}x} + Be^{-i\sqrt{{2mE \over \hbar^2}}x} $$
지난 시간에 정의한 $k^2 = {2mE \over \hbar^2}$이라는 식을 사용합시다. 이것을 위 식에 대입해 주겠습니다.
$$ \psi(L) = Ae^{ikL} - Ae^{-ikL} $$
이제 여기서 A와 B의 값을 구하기 위해 경계조건을 대입하겠습니다. Wave Function은 연속이고, 미분가능해야 하기 때문에 Potential이 $\infty$인 구간과 0인 구간이 만나는 지점에서 경계조건이 다음과 같이 성립합니다.
$$ \psi(0) = 0 $$
$$ \psi(L) = 0 $$
이것을 대입하게 되면 다음과 같은 식이 성립합니다.
$$ \psi(0) = 0 : A + B = 0 \cdot\cdot\cdot (1)$$
$$ \psi(L) = 0 : \psi(x) = Ae^{ikL} + Be^{-ikL} \cdot\cdot\cdot (2)$$
우리가 구하는 Wave Function은 실제 전자의 거동 특성을 의미하기 때문에 복소함수가 아닌 실함수여야합니다. Wave Function이 실함수가 되기 위해선 $Ae^{i\sqrt{{2mE \over \hbar^2}}L}$와 $Be^{-i\sqrt{{2mE \over \hbar^2}}L}$가 Conjugate 관계여야 합니다. 따라서 A와 B를 다음과 같이 치환합시다.
$$A = a + \imath b$$
$$B = a - \imath b$$
A와 B에 대한 식을 먼저 (1) 식에 대입합시다.
$$ A + B = a+\imath b + a - \imath b = 2a = 0 $$
$$ \therefore a = 0 $$
그리고 (2)식에 양변에 $e^{ikL}$를 곱해주면 다음과 같습니다.
$$ Ae^{i(2kL)} + B = 0 $$
여기서 $A +B = 0$이므로 B는 -A와 같습니다. 대입해줍시다.
$$ Ae^{i(2kL)} - A = A(e^{i(2kL)} - 1) = 0 $$
이 식이 성립하기 위해선 A = 0이거나 $e^{i(2kL)} -1 = 0$이어야 합니다. 하지만 A =0이 되어버리면 $\psi(x)$가 0이라는 값을 갖게 되는데 그것은 Quantum Well의 밖에도 안에도 입자가 존재할 확률이 0이 된다는 것을 의미합니다. 그런데 입자는 분명이 Quantum Well안에 존재하기 대문에 이것은 말이 안되는 것이죠. 따라서 다음과 같은 식이 성립해야 합니다.
$$ e^{i(2kL)} = 1 $$
$e^{i(2kL)}$가 1이 되기 위해선 2kx의 값이 0, $2\pi$, $4\pi$, ... 가 되어야 합니다. 즉 k값은 다음과 같습니다.
$$ k = {2n\pi \over 2k} = {n\pi \over L} $$
이렇게 구한 조건들을 활용해 Wave Function을 구해봅시다.
$$ \psi(x) = \imath b e^{ikx} -\imath b e^{-ikx} = \imath b (e^{ikx} - e^{-ikx})$$
여기서 오일러 공식을 이용하여 삼각함수로 바꾸어 보겠습니다.
(오일러 공식 : $ e^{iw} = cosw + \imath sinw$)
$$ \psi(x) = ib (e^{ikx} - e^{-ikx}) = ib (cos(kx) + isin(kx) - cos(-kx) - i sin(-kx))$$
이 때, cos은 우함수 sin은 기함수 이므로 다음과 같이 정리할 수 있습니다.
$$ \psi(x) = ib (cos(kx) +isin(kx) - cos(kx) + i sin(kx)) = ib(2isin(kx)) =-2bsin(kx)$$
이 때 -2b를 B'이라고 하면 다음과 같습니다.
$$ \psi(x) = -2bsin(kx) = B'sin({kx}) $$
현재 저희는 Potential Barrier가 $\infty$인 상황에서 문제를 풀고 있습니다. 상식적으로 Potential이 $\infty$라면, 전자가 그 장벽을 뚫고 지나갈 수가 없을 것입니다. 따라서 전자가 Potential Barrier를 뚫고 나갈 수가 없다는 조건 또한 사용할 수 있습니다.
이것은 전자가 x = 0과 x = L 사이에 무조건 존재할 수 밖에 없다는 뜻이 되기 때문에 다음과 같은 식이 성립합니다.
$$ \int_{0}^{L} |\psi(x)|^2 dx = 1 $$
이 식에 $\psi(x)$를 대입합시다.
$$ \int_{0}^{L} |B'sin(kx)|^2 dx = {B'}^2 \int_{0}^{L} {{1 + cos{kx \over 2} \over 2}} dx = {B'}^2\left[{{1\over2} + {1 \over 4k}sin(2kx)}\right]^L_0 = {L{B'}^2 \over 2} = 1$$
이것을 정리해보면 다음과 같습니다.
$$ B' = \sqrt{2 \over L} $$
이를 Wave Function에 대입합시다.
$$ \psi(x) = \sqrt{2 \over L} sin(kx) $$
여기에 $k = {n\pi \over L}$이라는 조건식을 대입하게 되면 최종적인 Wave Function을 얻을 수 있습니다.
$$ \psi(x) = \sqrt{2 \over L} sin({n\pi x \over L}) $$
지금 이렇게 복잡하게 풀었지만, 일반해를 $\psi(x) = Acos(kx) +Bsin(kx)$로 두고 풀게 되면 간단하게 같은 해를 얻을 수 있으며 좀 더 일반적인 방법입니다. 푸는 방법은 똑같으나 자유공간에서의 일반해와 같은 형태로 시작하기 위해 조금 더 복잡한 방법으로 풀이하였는데, 일반적인 방법을 이용해 각자 한번씩 해보시길 바랍니다.
자 이제 Infinite Quantum Well Problem을 풀어서 나온 해를 해석해봅시다. 그러기 위해선 아까 k값에서 부터 다시 시작해야 합니다.
$$ k = n\pi \over L $$
이 식에서 보면 k는 $\pi \over L$의 정수배임을 알 수 있습니다. 즉 k는 $\pi$를 Quantum Well의 길이로 나눈 값의 정수배입니다. 이는 k라는 값이 띄엄띄엄하게 양자화되어 있다는 것을 알 수 있습니다. 따라서 k는 n이라는 정수의 값에 따라 변하기 때문에 $k_n$으로 두도록 하겠습니다. 이를 수식으로 표현하게 되면 다음과 같습니다.
$$ k_n = {n\pi \over L} = \sqrt{2mE \over \hbar^2} $$
이 때 k값이 n에 따라 변하게 되면 E 또한 n에 따라 변하는 값이기 때문에 $E_n$이라고 할 수 있으며 수식으로 표현하면 다음과 같습니다.
$$ k_n = \sqrt{2mE_n \over \hbar^2} $$
그러면 이것을 $E_n$에 대해서 정리해보면, 다음과 같습니다.
$$ E_n = {\hbar^2k^2 \over 2m} = {\hbar^2 \over 2m}{n^2\pi^2 \over L^2} $$
위 식에서 Quantum Well의 폭이 정해져있다면, n을 제외한 값은 모두 상수입니다. 따라서 n의 값에 의해 k그래서 에너지 띠를 그려보게 되면 다음과 같이 띄엄띄엄 존재한다는 것을 확인할 수 있습니다.
(에너지띠 그림)
이렇게 입자가 갖는 에너지와 k값이 양자화되어 있음을 보였습니다. 그런데 왜 에너지의 양자화를 전혀 고려하지 않은 고전역학이 자연에서의 물체의 운동을 잘 설명할 수 있는 것일까요? 이유는 간단합니다.
자연에서 우리가 보는 물체는 전자나 원자핵같은 입자에 비해 굉장히 큽니다. 즉 Quantum Well의 크기가 커지게 되는 것이죠. 에너지와 k는 L값에 반비례하기 때문에, L값이 커지게 되면 에너지와 k값은 작아지게 될 것입니다. 따라서 여기에 몇 배를 해주더라도 크게 차이가 나지 않게 되는 것이죠. 한번 계산해봅시다.
질량이 500g이고 1m 길이인 물체가 갖는 Energy Level을 계산해보면 다음과 같습니다.
$$ E_1 = {{\hbar^2 \pi^2} \over 2mL^2} = {{{(10^{-31})}^2{\pi^2}} \over {2 * (10^{-34}) * {(10^{-10})}^2}} \simeq 10^{-67} J = 10^{-48}$$
$$ E_2 = 2^2 * {{\hbar^2 \pi^2} \over 2mL^2} = 2^2 *{{{(10^{-31})}^2{\pi^2}} \over {2 * (10^{-34}) * {(10^{-10})}^2}} \simeq 4 * 10^{-67} J = 4 * 10^{-48}$$
$$ E_3 = 3^2 * {{\hbar^2 \pi^2} \over 2mL^2} = 3^2 *{{{(10^{-31})}^2{\pi^2}} \over {2 * (10^{-34}) * {(10^{-10})}^2}} \simeq 9 * 10^{-67} J = 9 * 10^{-48}$$
1eV는 전자 한개가 1V의 전압을 거슬러 올라가기 위해 필요한 에너지이며 이는 매우 작은 에너지입니다. 여기에 4, 9, 16 등 여러 정수가 곱해지더라도 우리의 눈에는 거의 연속된 것처럼 보일 것입니다.
그렇다면 반대로 작은 물질은 어떨까요? 질량이 $10^{-31}kg$이고 크기가 $10^{-10}m$인 전자의 에너지를 계산해봅시다.
$$ E_1 = {{\hbar^2 \pi^2} \over 2mL^2} = {{{(10^{-34})}^2{\pi^2}} \over {2 * (10^{-31}) * {(10^{-10})}^2}} \simeq 10^{-17} J = 100 eV$$
$$ E_2 = 2^2 * {{\hbar^2 \pi^2} \over 2mL^2} = 2^2 *{{{(10^{-31})}^2{\pi^2}} \over {2 * (10^{-34}) * {(10^{-10})}^2}} \simeq 4 * 10^{-17} J = 400eV $$
$$ E_3 = 3^2 * {{\hbar^2 \pi^2} \over 2mL^2} = 3^2 *{{{(10^{-31})}^2{\pi^2}} \over {2 * (10^{-34}) * {(10^{-10})}^2}} \simeq 9 * 10^{-17} J = 900eV $$
위에서 큰 물체가 갖는 Energy level과 비교했을 때, 훨씬 큰 에너지를 가지며, 정수배를 했을 때 유의미한 차이가 나는 것을 확인할 수 있습니다.
이것을 통해 우리가 눈으로 보는 물체가 갖는 에너지는 실제로는 아주 작은 간격으로 양자화되어 있지만 우리가 보기에는 거의 연속적으로 고려해도 크게 차이가 나지 않는다는 것을 이해할 수 있습니다. 어떻게 보면 현재 우리가 살고 있는 거시세계에서도 우리는 양자역학을 적용해 왔다고 생각할 수도 있을 것 같습니다.
이로써 에너지의 양자화를 증명할 수가 있습니다.
또한 에너지와 k값이 n에 의해 결정되는 것처럼 Wave Function $\psi(x)$ 또한 정수 n에 의해 결정됩니다. 따라서 같은 방식으로 밑첨자 n을 사용하여 표현하면 다음과 같습니다.
$$ \psi_n(x) = \sqrt{2 \over L} sin({n\pi x \over L}) $$
이제 거리 x에 따라서 Wave Function이 어떻게 변하는지 그래프로 그려보도록 하겠습니다. 먼저 Potential이 $\infty$인 부분은 0이 되고요. n을 하나씩 증가시켜 가면서 그려보면 다음과 같습니다.
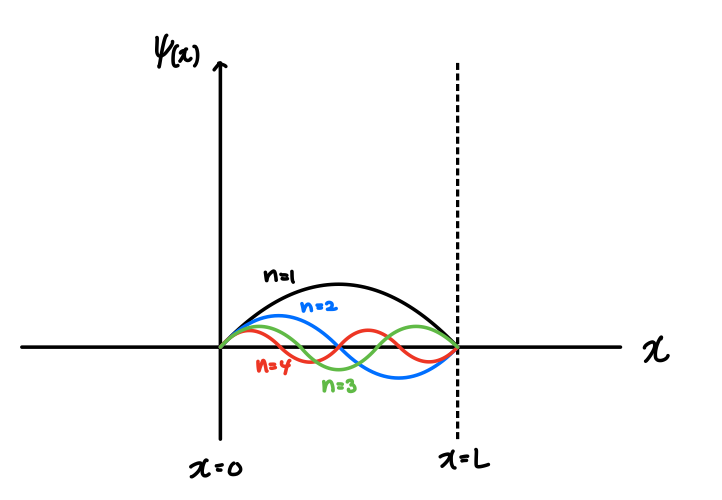
그러면 전자가 존재할 확률은 어떻게 될까요? 전자가 위치 x에 존재할 확률은 $|\psi(x)|^2$이니까 다음과 같이 그려질 것입니다.

위의 그래프를 양자화 된 Energy level위에다 그려보도록 하겠습니다.

위그래프에서 알 수 있는 사실은 매우 작은 입자가 Quantum Well에 존재할 때 Quantum Well 내부의 어디에서든 존재할 수 있으며 지점별로 존재할 확률이 다르다는 것입니다. 따라서 전자와 같은 매우 작은 입자의 위치를 설명할 땐 확률을 이용하여 표현할 수 밖에 없게 됩니다.
여기까지가 Infinite Quantum Well로부터 우리가 알아낼 수 있는 정보들 입니다. 다음 포스팅에서는 Potential Step과 Finite Quantum Well 내에서 전자가 어떻게 거동하는지 알아보도록 하겠습니다.
'전자공학 > 물리전자' 카테고리의 다른 글
| [물리전자] 2-2. Schrodinger Equation (0) | 2021.01.04 |
|---|---|
| [물리전자] 2-1. 양자역학 개념의 도입 (0) | 2021.01.04 |
| [물리전자] 1-5. Epitaxial Growth (0) | 2021.01.04 |
| [물리전자] 1-4. Silicon Wafer (0) | 2020.12.31 |
| [물리전자] 1-2. Unit Cell과 Lattice (2) | 2020.12.28 |






